Question

We observe the following annualized yields on four Treasury securities: (75%)

Maturity (years) Yield-to-maturity (%)
0.5 4.00
1 4.50
1.5 5.00
2 5.50
The par is $1000 for all the securities. The one with 0.5-year to mature is a zero coupon bond. Al other securities are coupon-bearing bonds selling at par. Note that, for par bonds, the coupon rate equals YTM. (20 points)
1. Calculate the spot rates for the maturities of 0.5, 1, 1.5, and 2 years.
2. What is the price of a 2-year bond with an 8% annual coupon rate (assume $1000 par)?
3. Suppose a 1-year zero-coupon bond with a par value of S1000 is selling at $900. Is there any arbitrage opportunity? If there is, construct an arbitrage portfolio and show the profit.
4. Calculate the one-period-ahead forward rates from 0 to 0.5, from 0.5 to 1, from 1 to 1.5, and from 1.5 to 2.
5. One year from now, you plan to purchase a then one-year bond with a 1000 par and an 8% annual coupon rate. What is the expected price of the bond? Assume the expectation hypothesis holds. Under the expectation hypothesis, the expected future spot rate equals the forward rate.

Answer 1

Step-by-step explanation:

1.

From the given information;

The spot rate for maturity at 0.5 year
`(X_1) = 4\%/2 = 2\%`

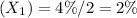
The spot rate for maturity at 1 year is:

=
`(22.5)/((1+X_1))+ (1000 + 22.5)/((1+X_2)^2)=1000`

=
`(22.5)/((1+0.02))+ (1000 + 22.5)/((1+X_2)^2)=1000`

=
`(22.5)/((1+0.02))+ (1022.5)/((1+X_2)^2)=1000`

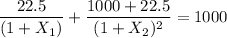
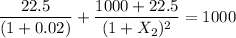
By solving for
`X_2`;

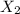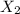`X_2` = 2.253%

The spot rate for maturity at 1.5 years is:

`= (25)/((1+X_1))+ (25)/((1+X_2)^2)+ (1000 + 25)/((1+X_3)^3)=1000`

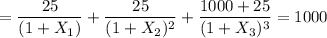
Solving for
`X_3`

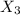
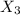`X_3` = 2.510%

The spot rate for maturity at 2 years is:

`= (27.5)/((1+X_1))+ (27.5)/((1+X_2)^2)+ (27.5)/((1+X_3)^3) +(1000+27.5)/((1+X_4)^4) =1000`

By solving for
`X_4`;

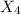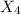`X_4` = 2.770%

Recall that:

Coupon rate = yield to maturity for par bond.

Thus, the annual coupon rates are 4%, 4.5%, 5%, and 5.5% for 0.5, 1, 1.5, 2 years respectively.

2.

For n years, the price of n-bond is:

`= (cash \ flow \ at \ year \ 1)/(1+X_1)+ (cash \ flow \ at \ year \ 2)/((1+X_2)^2)+... + (cash \ flow \ at \ year \ b)/((1+X_n)^n)`

Thus, for 2 years bond implies 4 periods;

∴

`= (40)/(1+0.02)+ (40)/((1+0.02253)^2) + (40)/((1+0.0252)^3)+ (40)/((1+0.0277)^4)`

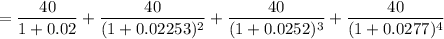
= $1047.024

3.

Suppose there exist no-arbitrage, then the price is:

`= (0)/((1+0.02))+(1000)/((1+0.02253)^2)`

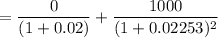
= 956.4183

Since the market price < arbitrage price.

We then consider 0.5, 1-year bonds from the portfolio

Now;

weight 2 × 1000 + weight 2 × 22.5 = 1000

weight 2 × 1022.5 = 1000

weight 2 = 1022.5/1000

weight 2 = 0.976

weight 1 + weight 2 = 1

weight 1 = 1 - weight 2

weight 1 = 1 - 0.976

weight 1 = 0.022

The price of a 0.5-year bond will be:

`= (1000)/((1+0.02\%)) \\ \\ =\mathbf{980.39}`

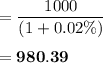
The price of a 1-year bond will be = 1000

Market value on the bond portfolio = 0.022 × price of 0.5 bond + 0.978 × price 1-year bond = 956.42

= 0.022 × 980.39 + 0.978 × 1000

= 956.42

So, to have arbitrage profit, the investor needs to purchase 1 unit of the 1-year zero-coupon bond as well as 0.022 units of the 0.5-year bond. Then sell 0.978 unit of the 1-year bond.

Then will he be able to have an arbitrage profit of $56.42

4.

The one-period ahead forward rates can be computed as follows:

Foward rate from 0 to 0.5
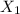`X_1` = 2%

Foward rate from 0.5 to 1

`(1+X_2)^2 = (1+X_1) * (1+ Foward \ rate \ from \ 0.5 \ to \ 1 )`

`(1+0.0225)^2 = (1+0.02) * (1+ Foward \ rate \ from \ 0.5 \ to \ 1 )`

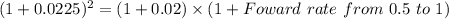
Foward rate from 0.5 to 1 = 2.5%

Foward rate from 1 to 1.5

`(1+X_3)^3 = (1+X_2)^2 * (1+ Foward \ rate \ from \ 1 \ to \ 1.5 )`

`(1+0.0251)^3 = (1+0.0225)^3 * (1+ Foward \ rate \ from \ 1 \ to \ 1.5 )`

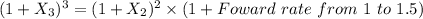
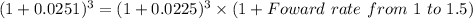
Foward rate from 1 to 1.5 =3.021%

Foward rate from 1.5 to 2

`(1+X_4)^4 = (1+X_3)^3 * (1+ Foward \ rate \ from \ 1.5 \ to \ 2 )`

`(1+0.0277)^4 = (1+0.0251)^3 * (1+ Foward \ rate \ from \ 1.5 \ to \ 2 )`

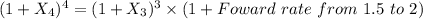
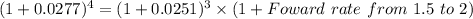
Foward rate from 1.5 to 2 =3.021%

5.

The expected price of the bond if the hypothesis hold :

=
`(40)/(1+ 0.03021)+ (1000+40)/((1+0.03285)^2)`

`= (40)/((1.03021))+ (1040)/((1.03285)^2)}`

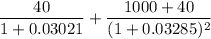
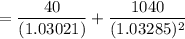
= 1013.724254

= 1013.72