Supposing that f((x + 1)/(x)) = (1)/(x^2) - 10, What is the value of f(46)?

Question

Supposing that
`f((x + 1)/(x)) = (1)/(x^2) - 10`,

What is the value of f(46)?

Answer 1

• The value of f(46) is 2015

------------------------

To find the value of f(46), we need to determine the value of x that makes the expression inside the function equal to 46.

So, we have:

`\cfrac{x + 1}{x} = 46`

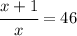
Now, we will solve for x.

Multiply both sides by x to get rid of the denominator:

• x + 1 = 46x
• 46x - x = 1
• 45x = 1
• x = 1/45

Now that we have the value of x, we can find the value of f(46) by plugging the x-value into the given equation:

`f(\cfrac{x + 1}{x}) = \cfrac{1}{x^2} - 10`

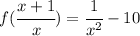
Plug in x = 1/45:

`f(46) = \cfrac{1}{(\cfrac{1}{45})^2} - 10`

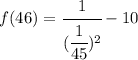
Now, simplify the expression:

`f(46) = \cfrac{1}{\cfrac{1}{2025} } -10`

`f(46) = 2025 - 10`

`f(46) = 2015`

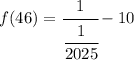
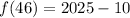
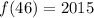
So, the value of f(46) is 2015.