Question

2. The length of a rectangular floor is 4 feet longer than its width w. The area of the floor is 165 ft2.

(a) Write a quadratic equation in terms of w that represents the situation. Show how you created it.

(b) Solve the quadratic equation using one of the methods covered in Unit 4 and then clearly state the dimensions of the floor in a sentence.

Show your work.

Answer 1

(a)

`W^2+4W-165=0`

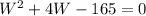
(b)

Width: 11 feet

Length: 15 feet

Explanation:

Given:

Width (W) = W ft

Length (L) = (4 + W) ft

Area (A) = 165 ft^2

(a)

The area of a rectangle is equal to the product of its length and width, therefore:

`A=L* W`

`\text{We replacing}`

`165=(4+W)*(W)`

`4W+W^2=165`

`W^2+4W-165=0`

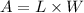
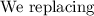
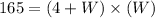
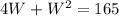
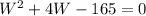
(b)

We solve the equation by factoring:

`W^2+4W-165=0`

`4W=-11W+15W`

`W^2-11W+15W-165=0`

`W(W-11)+15(W-11)=0`

`(W-11)(W-15)=0`

`W-11=0\rightarrow W=11`

`W+15=0\rightarrow W=-15`

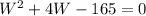
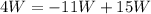
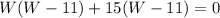
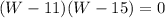
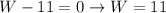
The width of the rectangle is equal to 11 feet and the length of the rectangle is equal to 15 feet.