Question

Use substitution to solve the system x-3y=10, x+5y=-22

Answer 1

• 
  `\bf x=-2`

• 
  `\bf y=-4`

Explanation:

To solve the given system, let's begin by solving for x in x- 3y=10:-

`\tt x-3y=10`

Add 3y to both sides:-

`\tt x-3y+3y=10+3y`

`\tt x=10+3y`

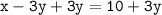
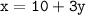
Substitute x= 10+3y into x+5y=-22:-

`\tt 10+3y+5y=-22`

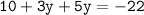
Simplify:-

`\tt 10+8y=-22`

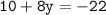
Now, solve for y in 10+8y=-22:-

`\tt 10+8y=-22`

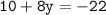
Subtract 10 from both sides:-

`\tt \tt 10+8y-10=-22-10`

`\tt 8y=-32`

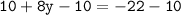
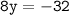
Divide both sides by -8:-

`\boxed{\bf y=-4}`

Now, substitute y=-4 into x=10+3y:-

`\tt x=10+3y`

`\tt x=10+3*-4`

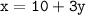
Simplify:-

`\boxed{\bf x=-2}`

Therefore, x=-2 and y=-4

_________________________

Hope this helps! :)

Answer 2

x = -2

y = -4

Explanation:

Given equations:

x - 3y = 10 --------------(1)

x + 5y = -22 -----------(2)

Taking Eq. (1)

x - 3y = 10

• Add 3y to both sides

x = 10 + 3y ------------(3)

• Put Eq. (3) in Eq. (1)

10 + 3y + 5y = -22

• Subtract 10 from both sides

8y = -22 - 10

8y = -32

• Divide 8 to both sides

y = -32/8

y = -4

• Put y = -4 in Eq. (3)

x = 10 + 3(-4)

x = 10 - 12

x = -2

`\rule[225]{225}{2}`