Question

Consider the infinite geometric series infinity sigma n=1 -4(1/3)^n-1. In this, the lower limit of the summation notion is "n=1". Please show your work I dont understand

Answer 1

a) The first four terms of the series are:

-4, -4/3, -4/9, -4/27

b) The series converges.

c) The sum of the infinite geometric series is -6.

Explanation:

Given infinite geometric series:

`\displaystyle \sum^(\infty)_(n=1) -4 \left((1)/(3)\right)^(n-1)`

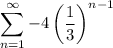
Therefore, the formula for the nth term of the sequence is:

`a_n=-4 \left((1)/(3)\right)^(n-1)`

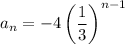
where:

• -4 is the first term, a.
• 1/3 is the common ratio, r.

The first four terms of the series can be found by substituting n = 1, 2, 3 and 4 into the nth term formula.

Therefore, the first four terms of the series are:

`a_1 = -4 \left((1)/(3)\right)^(1-1)=-4 \left((1)/(3)\right)^(0)=-4`

`a_2 = -4 \left((1)/(3)\right)^(2-1)=-4 \left((1)/(3)\right)^(1)=-(4)/(3)`

`a_3 = -4 \left((1)/(3)\right)^(3-1)=-4 \left((1)/(3)\right)^(2)=-4\left((1)/(9)\right)=-(4)/(9)`

`a_4 = -4 \left((1)/(3)\right)^(4-1)=-4 \left((1)/(3)\right)^(3)=-4 \left((1)/(27)\right)=-(4)/(27)`

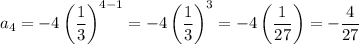
As the absolute value of the common ratio of the geometric series is less than 1, the sequence converges. Therefore, we can find the sum of the series by using the infinite sum formula:

`\boxed{S_(\infty)=(a)/(1-r), \;\;\; \text{for}\;|r| < 1}`

Substitute a = -4 and r = 1/3 into the formula to find the sum of the series:

`\begin{aligned}\implies S_(\infty)&=(-4)/(1-(1)/(3))\\\\ &=(-4)/((2)/(3))\\\\&=-4 \cdot (3)/(2)\\\\&=-(12)/(2)\\\\&=-6\end{aligned}`

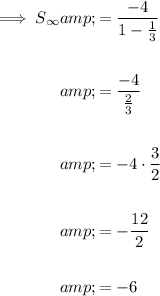
Therefore, the sum of the infinite geometric series is -6.