Question

Express cos R as a fraction in simplest terms.

Answer 1

`\cos(r) = (3)/(5)`

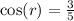
Explanation:

We need to evaluate cosR in simplest term . In a right angled triangle, we know that cosine is the ratio of base and hypotenuse. In the given right angled triangle, the longest side is 35 , so the hypotenuse is 35 , and with respect to angle R , base would be 21 and perpendicular would be 28 .

So in ∆PQR ,

`\implies \cos\theta = (b)/(h) \\`

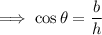
again, here base = 21 and hypotenuse= 35 , on substituting the respective values, we have;

`\implies \cos\theta =(21)/(35) \\`

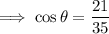
Here the angle is R , hence;

`\implies \cos\rm{R} =(21)/(35) \\`

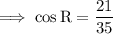
The HCF of 21 and 35 is , so on dividing numerator and denominator by 7 , we have ;

`\implies \underline{\underline{\red{\cos\rm{R} =(3)/(5)}}} \\`

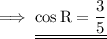
Hence the required answer is 3/5 .

Answer 2

`\cos R=(3)/(5)`

Explanation:

To find the cosine of an angle in a right triangle, use the cosine trigonometric ratio.

`\boxed{\begin{minipage}{9 cm}\underline{Cos trigonometric ratio} \\\\$\sf \cos(\theta)=(A)/(H)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

From inspection of the given right triangle PQR, the side adjacent to angle R is QR, and the hypotenuse is PR. Therefore:

• θ = R
• A = QR = 21
• H = PR = 35

Substitute these values into the formula:

`\implies \cos R=(21)/(35)`

To reduce the fraction to its simplest form, divide the numerator and denominator by their highest common factor (HCF).

The HCF of 21 and 35 is 7. Therefore:

`\implies \cos R=(21 / 7)/(35 / 7)=(3)/(5)`

Therefore, cos R expressed as a fraction in simplest terms is:

`\boxed{\cos R=(3)/(5)}`