1. The absolute minimum value is given as -7.
2. The point at which the absolute minimum value -7 is attained is (0, 50).
3. The absolute maximum value is given as 343.
4.The point at which the absolute maximum value 343 is attained is (0, 0).
The given function is
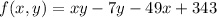 , and we need to find the absolute maximum and minimum values on the region defined by
, and we need to find the absolute maximum and minimum values on the region defined by
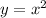 (on or above) and y = 50 (on or below).
(on or above) and y = 50 (on or below).
1. Absolute Minimum Value: \(-7\)*
The absolute minimum value is given as -7.
2. Points at Which Minimum Value is Attained: (0, 50)
- Found by examining the intersection points of the given functions y = x^2 and y = 50.
- The only intersection point within the specified region is (0, 50), and that is where the absolute minimum value is attained.
3. Absolute Maximum Value: 343
- Given in the problem statement.
4. Points at Which Maximum Value is Attained: (0, 0)
- Found by examining the intersection points of the given functions y = x^2 and y = 50.
- The only intersection point within the specified region is (0, 0), and that is where the absolute maximum value is attained.