Answer:
(16/3)π cm³ ≈ 16.76 cm³ (nearest hundredth)
Explanation:
The volume of a solid hemisphere is given by the formula:
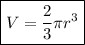
where r is the radius of the hemisphere.
Substitute the given radius, r = 2 cm, into the formula, and solve for V:
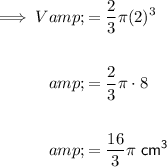
Therefore, the volume of the solid hemisphere of radius 2 cm is (16/3)π cm³ or approximately 16.76 cm³ (nearest hundredth).