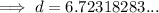Answer:
The point on the graph that is closest to the point (8, 1.5) is:
![\left(\sqrt[3]{4}, 2 \sqrt[3]{2}+1\right) \approx \left(1.587,3.520)](https://img.qammunity.org/2024/formulas/mathematics/college/o6566bh1ikta593khi7sdfoert5c37aexp.png)
Explanation:
To find the point on the graph of y = x² + 1 that is closest to the point (8, 1.5), we need to find the point on the parabola that is at the shortest distance from (8, 1.5). We can use the distance formula to do this.

Any point (x, y) on the parabola y = x² + 1 can be defined as (x, x²+1).
Therefore:
- (x₁, y₁) = (8, 1.5)
- (x₂, y₂) = (x, x²+1)
Substitute these points into the distance formula to create an equation for the distance between any point on the parabola and (8, 1.5):
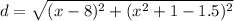
Simplifying this expression for d², we get:
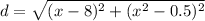
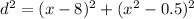
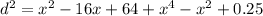
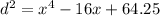
To find the x-coordinate that will minimize this distance, take the derivative of the expression with respect to x, set it equal to zero and solve for x:
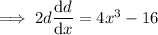
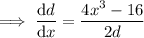
Set it equal to zero and solve for x:
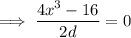
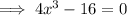
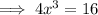
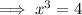
![\implies x=\sqrt[3]{4}](https://img.qammunity.org/2024/formulas/mathematics/college/mg9xhd5vas4gpx6dvyentn2hmnie32d037.png)
Finally, to find the y-coordinate of the point on the graph that is closest to the point (8, 1.5), substitute the found value of x into the equation of the parabola:
![\implies y=\left(\sqrt[3]{4}\right)^2+1](https://img.qammunity.org/2024/formulas/mathematics/college/tscc60h6ck1zt562u4fj5yb9w1nby50gwc.png)
![\implies y=\sqrt[3]{4^2}+1](https://img.qammunity.org/2024/formulas/mathematics/college/ddqvn5o9gcw3fux90gzyqtp5yjp7bjdch0.png)
![\implies y=\sqrt[3]{16}+1](https://img.qammunity.org/2024/formulas/mathematics/college/il9boxd3h0t6g5injlya69d2pes8bnk785.png)
![\implies y=\sqrt[3]{2^3 \cdot 2}+1](https://img.qammunity.org/2024/formulas/mathematics/college/hdpqp492pdatdoomxo6cvvkwgz13qmevi6.png)
![\implies y=\sqrt[3]{2^3} \sqrt[3]{2}+1](https://img.qammunity.org/2024/formulas/mathematics/college/r4w05yujmf9j9oe5d1z4a8h1zf1kn39ml5.png)
![\implies y=2 \sqrt[3]{2}+1](https://img.qammunity.org/2024/formulas/mathematics/college/3bouact2fnz3xw4asmc1c1wmnbiodvmbvu.png)
Therefore, the point on the graph that is closest to the point (8, 1.5) is:
![\left(\sqrt[3]{4}, 2 \sqrt[3]{2}+1\right) \approx \left(1.587,3.520)](https://img.qammunity.org/2024/formulas/mathematics/college/o6566bh1ikta593khi7sdfoert5c37aexp.png)
Additional information
To find the minimum distance between the point on the graph and (8, 1.5), substitute x = ∛4 into the distance equation:
![\implies d = \sqrt{(\sqrt[3]{4} - 8)^2 + ((\sqrt[3]{4})^2-0.5)^2}](https://img.qammunity.org/2024/formulas/mathematics/college/zx2ux341qezcvrja69e15kuw2xl2q82q2a.png)