Question

Which function models the area of a rectangle with side lengths of 2x – 4 units and x + 1 units? What is the area when x = 3?

A. f(x) = 2x2 – 4x + 4; A = 10 B. f(x) = 2x2 + 8x – 4; A = 38 C. f(x) = 2x2 – 8x + 4; A = 2 D. f(x) = 2x2 − 2x − 4; A = 8

Answer 1

Area of rectangle,
`f(x) = 2x^2 - 2x - 4`.

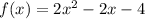Explanation:

We are given with side lengths of a rectangle are (2x-4) units and (x+1) units. It is required to find the area of rectangle.

The area of a rectangle is equal to the product of its length and breadth. It is given by :

`A=L* B`

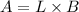
Let us consider, L = (2x-4) units and B = (x+1) units

Plugging the side lengths in above formula:

`A=(2x-4)*(x+1)`

`A = 2x^2 + 2x-4x - 4`

`A=2x^2-2x-4`

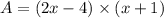
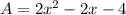
So, the function that models the area of a rectangle is
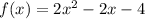`f(x) = 2x^2 - 2x - 4`.