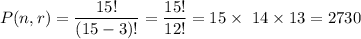Question

Question 24 (2 points)

Suppose a race takes place involving 15 participants. In how many different ways can
the top three finishers be arranged?
3
15
455
2730

Answer 1

`2730`

Explanation:

We can solve this problem without using any complex formulas, though there is a formula for solving such problems

Out of the 15 participants, only one participant can be in first place but this can be any one of the participants

So choice for first place = 15 participants

Once a participant has won in the first place, there are 14 remaining participants who can come second place

For third place there are only 13 participants who can make it

The total number of ways in which top three participants can be arranged is

15 x 14 x 13 = 2730 ways

The formula is

`P(n, r ) = (n!)/((n-r)!)`

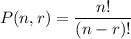
where n is the population to be considered; here n = 15

r = number of items to be considered ; here r = 3

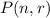`P(n, r)` sometimes written as
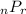`_nP_r` represents the number of subsets r that can be taken from a larger set n when the order of the subset matters.

using the formula we get


`P(n, r ) = (15!)/((15-3)!) = (15!)/(12!) = 15 * \ 14 * 13 = 2730`

Answer 2

Answer: The top three finishers can be arranged in 15 x 14 x 13 ways, since there are 15 choices for the first place, 14 choices for the second place (since one person has already been selected for first place), and 13 choices for the third place (since two people have already been selected for first and second place).

So the answer is:

15 x 14 x 13 = 2730

Therefore, the top three finishers can be arranged in 2730 different ways. Answer: 2730.

Explanation: