Question

17. The sum of the interior angles of a pentagon is6x + 6y. Find y in term of x

Answer 1

We know that, the sum of interior angles of an n-sided polygon is (n−2)×180⁰

For a pentagon, n=5

so,

`\implies \rm \: 6x + 6y = (n - 2)180`

`\implies \rm \: 6(x + y) = (5 - 2)180`

`\implies \rm \: 6(x + y )= 3 * 180`

`\implies \rm \: (x + y) = (3 * 180)/(6)`

`\implies \rm \: (x + y) = \frac{ 3 * \cancel{180} \: \:30}{ \cancel6}`

`\rm \implies \: x + y = 90`

`\underline{\boxed{\implies \rm \: y= 90 - x}}`

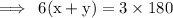
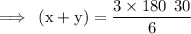
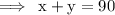
Pentagon Formulas

There are many formulas related to a pentagon. A few basic ones are given below.

• Diagonals of a pentagon: = n × (n − 3) ÷ 2 = 5 × (5 − 3) ÷ 2 = 5
• Sum of interior angles of a pentagon: = 180° × (n − 2) = 180° × (5 − 2) = 540°
• Each exterior angle of a regular pentagon: = 360° ÷ n = 360° ÷ 5 = 72°
• Each interior angle of regular pentagon: = 540° ÷ n = 540° ÷ 5 = 108°
• Area of a regular Pentagon = 1/2 × Perimeter × Apothem
• Perimeter of Pentagon = (side 1 + side 2 +side 3 + side 4 + side 5)