Question

Write the polynomial in factored form. Check by multiplication.

x³-6x² - 7x
x³-6x² - 7x= ?
(Factor completely.)

Answer 1

`p(x)=(x+5)(x-3)(x+4)`

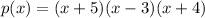
Explanation:

Given :
`p(x)=x^3+6x^2-7x-60`

Solution :

Part A:

First find the potential roots of p(x) using rational root theorem;

So,
`\text{Possible roots = }\pm\frac{\text{factors of constant term}}{\text{factors of leading coefficient}}`

Since constant term = -60

Leading coefficient = 1

`\text{Possible roots = }\pm\frac{\text{factors of 60}}{\text{factors of 1}}`

`\text{Possible roots = }\pm\frac{\text{1,2,3,4,5,6,10,12,15,20,60}}{\text{1}}`

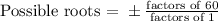
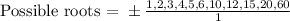
Thus the possible roots are
`\pm1,\pm2,\pm3,\pm4,\pm5,\pm6,\pm10,\pm12,\pm15,\pm20,\pm60`

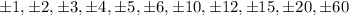
Thus from the given options the correct answers are -10, -5, 3, 15

Now For Part B we will use synthetic division

Out of the possible roots we will use the root which gives remainder 0 in synthetic division :

Since we can see in the figure With -5 we are getting 0 remainder.

Refer the attached figure

We have completed the table and have obtained the following resulting coefficients: 1 , 1,−12,0. All the coefficients except the last one are the coefficients of the quotient, the last coefficient is the remainder.

Thus the quotient is

And remainder is 0 .

So to get the other two factors of the given polynomial we will solve the quotient by middle term splitting

`x^2+x-12=0`

`x^2+4x-3x-12=0`

`x(x+4)-3(x+4)=0`

`(x-3)(x+4)=0`

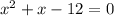
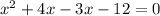
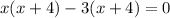
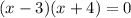
Thus x - 3 and x + 4 are the other two factors

So, p(x)=(x+5)(x-3)(x+4)