Question

Can you help me please it is urgent ..♥️
Me pueden ayudar por favor es urgente ♥️​

Answer 1

6. | Inequality | Boundary Line | Dot on Number Line |

|
`$9 > 2x+3$` | Solid | Open |

|
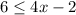`$6\le4x-2$` | Solid | Closed |

|
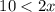`$10 < 2x$` | Dashed | Open |

7. Two inequalities, y < -3 and y > 4. Shade regions below -3 and above 4. Combine shaded areas for the solution.

6. For the first inequality, 9>2x+3, the boundary line is solid and the dot is open. This is because the inequality is strict, meaning that x cannot be equal to the value that makes the expression equal to zero. In this case, the value that makes the expression equal to zero is
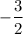`$-(3)/(2)$`, so x must be less than
`$-(3)/(2)$`.

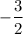For the second inequality,
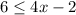`$6\le4x-2$`, the boundary line is solid and the dot is closed. This is because the inequality is non-strict, meaning that x can be equal to the value that makes the expression equal to zero. In this case, the value that makes the expression equal to zero is 1, so x can be less than or equal to 1.

For the third inequality, 10<2x, the boundary line is dashed and the dot is open. This is because the inequality is strict, meaning that x cannot be equal to the value that makes the expression equal to zero. In this case, the value that makes the expression equal to zero is 5, so x must be less than 5.

Here is the completed table:

| Inequality | Boundary Line | Dot on Number Line |

|
`$9 > 2x+3$` | Solid | Open |

|
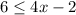`$6\le4x-2$` | Solid | Closed |

|
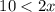`$10 < 2x$` | Dashed | Open |

7. First, solve each inequality separately. For the first inequality, -3y > 9, divide both sides by -3 and flip the direction of the inequality because you're dividing by a negative number. This gives you y < -3. For the second inequality, 2y - 6 > 2, add 6 to both sides and then divide both sides by 2 to get y > 4.

Now, you have two simple inequalities: y < -3 and y > 4. To graph these, draw a number line. Mark the points -3 and 4 with open circles, since they are not part of the solution sets. Then, shade the regions to the left of -3 and the right of 4. This is because the first inequality says that y must be less than -3, and the second inequality says that y must be greater than 4.

The final step is to combine the two shaded regions. Since the "or" in the compound inequality means that either one or both of the inequalities can be true for a number to be in the solution set, the solution is the union of the two shaded regions. This is the region that is shaded to the left of -3 and the right of 4.