Question

6.1.2 Exam: Semester 2 Exam

Question 17 of 34
Which triangle results from a reflection across the line x = 1?
4-3-2
O A.
2 A
4
1234
B
-54-3-2
3
B
4
+4
2
4
5
A'
X
1234
S
X

Answer 1

After reflection across
`\(x = 1\)`, the triangle's vertices (4, 3) and (2, 4) move left of
`\(x = 1\)` becoming (-2, 3) and (0, 4), respectively, while (1, 2) remains unchanged.

Given the triangle with vertices at (4, 3), (2, 4), and (1, 2), we want to reflect it across the line
`\(x = 1\)` to find the new coordinates.

To reflect a point across a vertical line like
`\(x = 1\)`:

Points to the left of
`\(x = 1\)` will move to the right side by the same distance.

Points to the right of
`\(x = 1\)` will move to the left side by the same distance.

Points on the line itself
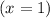`(\(x = 1\))` will remain unchanged.

Let's find the new coordinates for each point of the triangle.

(4, 3) is to the right of
`\(x = 1\)`. To find its reflection:

The distance between the point and the line
`\(x = 1\)` is 3 units.

So, the same distance to the left side of
`\(x = 1\)` will be the new x-coordinate:
`\(1 - 3 = -2\)`.

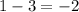The y-coordinate remains unchanged.

Therefore, the reflection of (4, 3) across
`\(x = 1\)` is (-2, 3).

(2, 4) is also to the right of
`\(x = 1\)`. Its reflection:

- The distance from (2, 4) to
`\(x = 1\)` is 1 unit.

- The same distance to the left side of
`\(x = 1\)`will be the new x-coordinate:
`\(1 - 1 = 0\)`.

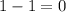- The y-coordinate remains unchanged.

Hence, the reflection of (2, 4) across
`\(x = 1\)` is (0, 4).

(1, 2) lies on the line and thus will remain unchanged after the reflection.

So, after reflecting the triangle across the line
`\(x = 1\)`, the new coordinates are (-2, 3), (0, 4), and (1, 2).

complete the question

A triangle has vertices at (4, 3), (2, 4), and (1, 2). What are the new coordinates of the triangle's vertices when it is reflected across the line \(x = 1\)?