Question

19x-3

8x+10
Find the measure of each angle

Answer 1

The answer is that the measure of angle A is
`\( (2968)/(27) \) degrees, and the measure of angle B is \( (1313)/(27) \) degrees, with \( x = (173)/(27) \).`

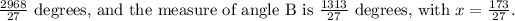
To determine the measures of angles A and B, we set up an equation based on the fact that supplementary angles add up to 180 degrees. Angle A is represented by
`\(19x - 3\) and angle B by \(8x + 10\). Combining these expressions, we have \(19x - 3 + 8x + 10 = 180\). Simplifying further, \(27x + 7 = 180\), and solving for x yields \(x = (173)/(27)\).`

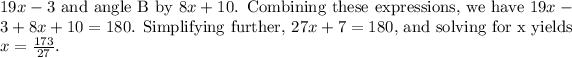
Substituting this value of x back into the expressions for A and B, we find that the measure of angle A is
`\(19 * (173)/(27)`
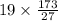
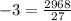`- 3 = (2968)/(27)\)`degrees, and the measure of angle B is
`\(8 * (173)/(27) + 10 = (1313)/(27)\) degrees.`

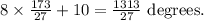
Therefore, the solution indicates that when \(x\) is
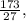`\((173)/(27)\),`angle A measures \
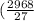`((2968)/(27)\)` degrees, and angle B measures
`\((1313)/(27)\)` degrees. This satisfies the condition that the two angles are supplementary, with their sum equaling 180 degrees.

The probable question maybe:

If the measure of angle A is given by
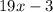`\(19x - 3\)` and the measure of angle B is
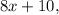`\(8x + 10\),`and the angles are supplementary, what is the measure of each angle?