The final velocity of the car is
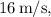 and the displacement is
and the displacement is
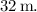
To find the final velocity and displacement of the car, you can use the kinematic equations. The two relevant equations are:
1. Final Velocity
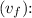
![\[ v_f = v_i + a \cdot t \]](https://img.qammunity.org/2024/formulas/physics/high-school/18fc06k9qsbjl9yw0risajlaccgo1ddfp0.png)
where
 is the initial velocity (assumed to be 0 m/s because the car starts from rest), \(a\) is the acceleration, and \(t\) is the time.
is the initial velocity (assumed to be 0 m/s because the car starts from rest), \(a\) is the acceleration, and \(t\) is the time.
2. Displacement

![\[ s = v_i \cdot t + (1)/(2) \cdot a \cdot t^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/bf6vzk3wogstyd9ct26cimcub413p6vihv.png)
where
 is the initial velocity,
is the initial velocity,
 is the acceleration, and \(t\) is the time.
is the acceleration, and \(t\) is the time.
Given that the car starts from rest
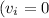 ), the acceleration
), the acceleration
 is
is
 and the time (\(t\)) is \(4 \, \text{s}\), you can substitute these values into the equations.
and the time (\(t\)) is \(4 \, \text{s}\), you can substitute these values into the equations.
1. Final Velocity
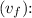
![\[ v_f = 0 + (4 \, \text{m/s}^2 \cdot 4 \, \text{s}) \]](https://img.qammunity.org/2024/formulas/physics/high-school/jgcob3k9a7r21df9fxiva4didn49k9av2z.png)
![\[ v_f = 16 \, \text{m/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/a4m5t12uzp6ih3tnlj96xtzn5dxl5tomnw.png)
2. Displacement (\(s\)):
![\[ s = 0 \cdot 4 + (1)/(2) \cdot 4 \, \text{m/s}^2 \cdot (4 \, \text{s})^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/qct7wwdbl5nf2uembs1sd8wuja5podzzm5.png)
![\[ s = 32 \, \text{m} \]](https://img.qammunity.org/2024/formulas/physics/high-school/zvwhxtjvr6t18gtbmftrwsrod4uxupf9hf.png)
Therefore, the final velocity of the car is
