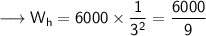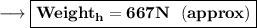Answer:
667 N
Step-by-step explanation:
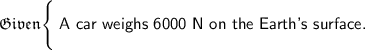
And we need to find out the weight of the car at a distance equal to 3 times the radius of the earth , from the centre of the earth.
We can find the acceleration due to gravity at a height h from the earth's surface as ,
![\sf\longrightarrow \red{ g_h = g\bigg[ 1 +(h)/(R_e)\bigg]^(-2)}](https://img.qammunity.org/2023/formulas/physics/high-school/46zfntlopcyntb4h6emyjmwlbn82ufqtph.png)
- The height here will be 3R - R = 2R , since 3R is the distance from the centre of the earth .
In above equation multiply both sides by m ,
![\sf\longrightarrow mg_h = mg\bigg[ 1 +(h)/(R_e)\bigg]^(-2)](https://img.qammunity.org/2023/formulas/physics/high-school/cigismzeqgoejatnxb1pv6hx741d57wndv.png)
Now here at the place of mg we can substitute 6000N , and mg
 will be the weight at height h which we are interested in finding .
will be the weight at height h which we are interested in finding .
![\sf\longrightarrow W_h = 6000 \bigg[ 1 +(2R)/(R)\bigg]^(-2)\\](https://img.qammunity.org/2023/formulas/physics/high-school/ssgdrwgvkx5t80q8426in87zv2v6vwnev7.png)
![\sf\longrightarrow W_h = 6000 [ 1 + 2 ]^(-2)\\](https://img.qammunity.org/2023/formulas/physics/high-school/4889jw6o5dznzfwtpwd2ra207sqzh2fvjp.png)
![\sf\longrightarrow W_h = 6000 [ 3]^(-2)\\](https://img.qammunity.org/2023/formulas/physics/high-school/jeozmjom5e7o5ipkdi83e44xv7xm2kbjpn.png)