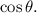For
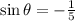 and
and
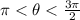 ,
,
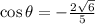 , derived using the Pythagorean identity and considering the third quadrant.
, derived using the Pythagorean identity and considering the third quadrant.
Given:
![\[ \sin \theta = -(1)/(5) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qurem6knrmyzaaylcxlf42xkppqno0i3xl.png) and
and
![\[ \pi < \theta < (3\pi)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/irssjg5j3hco9hsw3mste7l5hmp5rkg3p6.png)
Using the Pythagorean identity:
![\[ \cos^2 \theta = 1 - \sin^2 \theta \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rbumssoo3fr4by2amjtm2rkhae1qhg3u3c.png)
![\[ \cos^2 \theta = 1 - \left(-(1)/(5)\right)^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/3xaii7h1rz02caihc3i0h4o1p6135pm0gc.png)
![\[ \cos^2 \theta = 1 - (1)/(25) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/jgcnm0ecrclw1rlur3xcb909ve342fi7q4.png)
![\[ \cos^2 \theta = (24)/(25) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/aqqfu8s441bflmy5t8mt16p1sti40xgik4.png)
Taking the square root of both sides (as \( \theta \) lies in the third quadrant where cosine is negative):
![\[ \cos \theta = -\sqrt{(24)/(25)} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/186e7rvy3evbj4ak6sasznw0sd8eifohvk.png)
![\[ \cos \theta = -(√(24))/(√(25)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/myhne8liqgjgbmbngbervr7glow2tr71t8.png)
![\[ \cos \theta = -(2√(6))/(5) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/e5zj4eyt823n5bpzlslf3ijev6gtjmzh3p.png)
Therefore, when
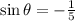 and
and
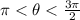 ,
,
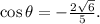
complete the question
To determine
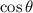 given
given
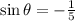 and
and
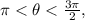 the Pythagorean identity for trigonometric functions and
the Pythagorean identity for trigonometric functions and
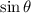 to solve for
to solve for