The slope of the line passing through the given points is
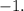
Certainly! Let's calculate the slope using the given points (x, y):
![\[ \text{Slope} = (y_2 - y_1)/(x_2 - x_1) \]](https://img.qammunity.org/2024/formulas/mathematics/college/1tiyzjfutzek4plzqt3yl4u45zxklq27xt.png)
Let's choose the points (5, -5) and (8, -8) from the given set:
![\[ \text{Slope} = ((-8) - (-5))/((8) - (5)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/k0uadl8inmnwgekwgb1znmj2jfsuxnqevr.png)
![\[ \text{Slope} = (-3)/(3) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/auu1l8wpm08wuzh7ty8kt2lpwen3k5sknf.png)
![\[ \text{Slope} = -1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/uqtaot5fe1rjvr60k3km7yhf1ss64vxagj.png)
So, the slope of the line passing through the given points is
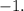
The probable question maybe:
Certainly! Here's a meaningful question related to the given statement:
Question: Given the points (x, y) where x values are 5, 6, 7, and 8, and corresponding y values are -5, -6, -7, and -8, what is the slope of the line passing through these points?
This question can be answered by applying the formula for calculating the slope (\(m\)) between two points
 , which is given by:
, which is given by:
![\[ m = \frac{{y_2 - y_1}}{{x_2 - x_1}} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2qggmkbwy3fln1sw6or7un76nopoa3le1l.png)
In this case, you can choose any two points from the given set of (x, y) values and substitute them into the formula to find the slope.