Final Answer:
A reasonable value for the diffusion coefficient
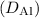 of aluminum in silicon at 400 K can be estimated using the Arrhenius equation. Assuming an activation energy (Q) of 1.2 eV, the diffusion coefficient at 400 K
of aluminum in silicon at 400 K can be estimated using the Arrhenius equation. Assuming an activation energy (Q) of 1.2 eV, the diffusion coefficient at 400 K
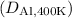 is approximately
is approximately
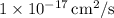 .
.
Step-by-step explanation:
The Arrhenius equation relates the diffusion coefficient (D) to temperature (T) through the formula
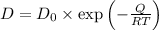 , where \(D_0\) is a pre-exponential factor, (Q) is the activation energy, (R) is the gas constant, and (T) is the absolute temperature. To estimate
, where \(D_0\) is a pre-exponential factor, (Q) is the activation energy, (R) is the gas constant, and (T) is the absolute temperature. To estimate
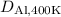 , we can rearrange the equation as
, we can rearrange the equation as
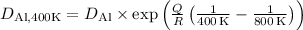 .
.
Given
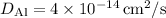 at 800 K, assuming (Q = 1.2) eV, and using
at 800 K, assuming (Q = 1.2) eV, and using
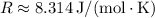 , we find
, we find
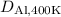 to be approximately
to be approximately
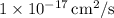 . This lower value at 400 K is expected due to the exponential temperature dependence of diffusion coefficients.
. This lower value at 400 K is expected due to the exponential temperature dependence of diffusion coefficients.
In materials science, such calculations are crucial for understanding diffusion processes at different temperatures, providing insights into material behavior and aiding in the design and optimization of electronic devices and other applications.