Question

jessica opened a bank account that earns 222 percent interest compounded annually. her initial deposit was $100$100dollar sign, 100, and she uses the expression $100()$100(x) t dollar sign, 100, (, x, ), start superscript, t, end superscript to find the value of the account after tt (calculator ok) questionsquestion 37 of 38reportwhat is the value of xx in the expression?

Answer 1

Jessica's account grows with compound interest at 222%. The expression
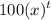`$100(x)^t$`indicates
`\(x\)` as the factor by which $100 compounds annually. Here,
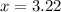`\(x = 3.22\)` represents the multiplication factor for each year over
`\(t\)` years.

Given:

Principal amount
`(\(P\))`= $100

Annual interest rate
`(\(r\))` = 222%

The formula for compound interest is given by:

`\[ A = P * (1 + r)^t \]`

Where:

`\( A \)` is the final amount after
`\( t \)` years

`\( P \)` is the principal amount (initial deposit)

`\( r \)` is the annual interest rate in decimal form

`\( t \)` is the time the money is invested for

First, convert the annual interest rate from percentage to decimal:

`\[ r = (222)/(100) = 2.22 \]`

Now, the expression given is
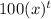`\(100(x)^t\)`, suggesting that
`\(x\)` is the factor by which the initial deposit
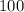`\(100\)` is multiplied each year for
`\(t\)` years to find the final value of the account.

Comparing the compound interest formula and the expression
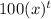`\(100(x)^t\)`, we equate
`\(x\)` with
`\((1 + r)\).`

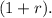
Therefore,
`\(x = 1 + 2.22 = 3.22\).`

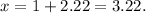
Thus, in the expression
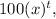`\(100(x)^t\),` the value of
`\(x\)` is
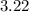`\(3.22\)`. This signifies that the initial deposit is multiplied by 3.22 each year for
`\(t\)` years to calculate the account's final value.

complete the question

Jessica deposited $100 into a bank account that accrues compound interest at a rate of 222% annually. If she uses the expression $100(x)^t$ to represent the account value after \(t\) years, what is the value of \(x\) in the expression?