Question

a 10-g bullet moving horizontally at penetrates a 3.0-kg wood block resting on a horizontal surface. if the bullet slows down to after emerging from the block, what is the speed of the block immediately after the bullet emerges

Answer 1

The block's final speed is
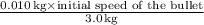`\( \frac{0.010 \, \text{kg} * \text{initial speed of the bullet}}{3.0 \, \text{kg}} \)` after a 10-g bullet penetrates a 3.0-kg wood block, coming to rest.

To solve this problem, we can use the principle of conservation of linear momentum. The total linear momentum before the collision is equal to the total linear momentum after the collision.

The linear momentum (p) is given by the product of mass and velocity
`(p = m * v).`

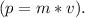
Before the collision:

`\[ \text{Momentum of bullet} = m_{\text{bullet}} * v_{\text{bullet\_initial}} \]`

`\[ \text{Momentum of block} = m_{\text{block}} * v_{\text{block\_initial}} \]`

After the collision:

`\[ \text{Momentum of bullet} = m_{\text{bullet}} * v_{\text{bullet\_final}} \]`

`\[ \text{Momentum of block} = m_{\text{block}} * v_{\text{block\_final}} \]`

The total linear momentum before the collision is equal to the total linear momentum after the collision:

`\[ m_{\text{bullet}} * v_{\text{bullet\_initial}} + m_{\text{block}} * v_{\text{block\_initial}} = m_{\text{bullet}} * v_{\text{bullet\_final}} + m_{\text{block}} * v_{\text{block\_final}} \]`

Now, substitute the given values:

`\[ (0.010 \, \text{kg}) * v_{\text{bullet\_initial}} + (3.0 \, \text{kg}) * 0 = (0.010 \, \text{kg}) * 0 + (3.0 \, \text{kg}) * v_{\text{block\_final}} \]`

Since the block is initially at rest
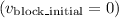`(\(v_{\text{block\_initial}} = 0\))` and the bullet comes to rest after penetrating the block
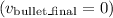`(\(v_{\text{bullet\_final}} = 0\))` , the equation simplifies to:

`\[ (0.010 \, \text{kg}) * v_{\text{bullet\_initial}} = (3.0 \, \text{kg}) * v_{\text{block\_final}} \]`

Now, solve for \(v_{\text{block\_final}}\):

`\[ v_{\text{block\_final}} = \frac{0.010 \, \text{kg} * v_{\text{bullet\_initial}}}{3.0 \, \text{kg}} \]`

Insert the given value for
`\(v_{\text{bullet\_initial}}\), and calculate \(v_{\text{block\_final}}\).`

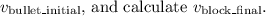
Note: Make sure to use consistent units, and the final result will be in meters per second (m/s).