Question

Consider the system x ′ =[ −1 1

0​ 1​ ] x
(a) Find the general solution for the system.
(b) Using your general solution, state a fundamental matrix X(t) for the system. Verify that X(t) is indeed a fundamental matrix.
(c) Is the equilibrium solution
0 a source, sink or saddle? Is it unstable or stable? Explain.
(d) Sketch the phase portrait.

Answer 1

To find the general solution for the given system, we need to find the eigenvalues and eigenvectors of the coefficient matrix. Once we have the eigenvalues and eigenvectors, we can express the general solution using exponential functions.

Step-by-step explanation:

To find the general solution for the given system x' = [-1 1 0; 1]x, we need to find the eigenvalues and eigenvectors of the coefficient matrix. The eigenvalues are obtained by solving the characteristic equation, det(A - λI) = 0, where A is the coefficient matrix. The eigenvectors are then found by solving the equation (A - λI)x = 0. Once we have the eigenvalues and eigenvectors, we can express the general solution as
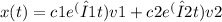`x(t) = c1e^(λ1t)v1 + c2e^(λ2t)v2`nd λ1 and λ2 are the eigenvalues corresponding to the eigenvectors v1 and v2, respectively.