Final Answer:
(i) Meaningful. curl f is a vector field.
(ii) Meaningful. grad f is a vector field.
(iii) Meaningful. div F is a scalar field.
(iv) Meaningful. curl(grad f) is a vector field.
(v) Meaningful. grad F is a vector field.
(vi) Not meaningful. grad div F involves taking the gradient of a scalar, resulting in a vector field.
(vii) Not meaningful. div(grad f) involves taking the divergence of a vector, resulting in a scalar field.
(viii) Not meaningful. grad(div f) involves taking the gradient of a scalar, resulting in a vector field.
(ix) Meaningful. curl(curl F) is a vector field.
(x) Not meaningful. div(div F) involves taking the divergence of a scalar, resulting in a scalar field.
(xi) Not meaningful. (grad f) × (div F) involves the cross product of a vector and a scalar, which is not defined.
(xii) Meaningful. div(curl(grad f)) is a scalar field.
Step-by-step explanation:
In vector calculus, the operations of gradient (grad), divergence (div), and curl are fundamental. The curl of a scalar field \(f\) (i) results in a vector field, while the gradient of a scalar field \(f\) (ii) is itself a vector field. Similarly, the divergence of a vector field \(F\) (iii) results in a scalar field.
However, certain combinations are not meaningful. For instance, taking the gradient of a scalar (vi) or the divergence of a vector (vii) results in undefined operations. Similarly, the combination of taking the gradient of the divergence of a vector (viii) or the divergence of the divergence of a vector (x) lacks meaningful interpretations.
On the other hand, operations like curl(curl F) (ix) and
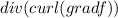 (xii) are meaningful and result in vector and scalar fields, respectively. Understanding the properties and meanings of these vector calculus operations is essential in various fields, including physics, engineering, and computer science.
(xii) are meaningful and result in vector and scalar fields, respectively. Understanding the properties and meanings of these vector calculus operations is essential in various fields, including physics, engineering, and computer science.