Ross can fill the water balloon for approximately 11.34 seconds before it pops, given the constraints.
How did we get the value?
Calculate
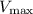 :
:
![\[ R = 5 \, \text{inches} \]](https://img.qammunity.org/2022/formulas/mathematics/college/65jmb3knmxts9577c09gsjnlq7k0vujz3v.png)
![\[ V_{\text{max}} = (4)/(3)\pi * (5^3) \]](https://img.qammunity.org/2022/formulas/mathematics/college/r1hse08clwdtcmbtchoo8x6md514oail64.png)
![\[ V_{\text{max}} = (4)/(3)\pi * 125 \]](https://img.qammunity.org/2022/formulas/mathematics/college/ymbj24jyo54vcoj2y35mf42tl1vvd3biyy.png)
![\[ V_{\text{max}} \approx 523.8 \, \text{cubic inches} \]](https://img.qammunity.org/2022/formulas/mathematics/college/dcjkbl2389rntin4994qeg29cfvo6ysmnd.png)
Convert the flow rate to cubic inches per minute:
![\[ \text{Flow rate} = 12 \, \text{gallons/minute} * 231 \, \text{cubic inches/gallon} \]](https://img.qammunity.org/2022/formulas/mathematics/college/v00wzhv058deujb4kvvnebswjgp5sw538r.png)
![\[ \text{Flow rate} \approx 2772 \, \text{cubic inches/minute} \]](https://img.qammunity.org/2022/formulas/mathematics/college/fjk6tqffn4ok583zlkaref850redtmavko.png)
Calculate the time in minutes:
![\[ \text{Time (minutes)} = \frac{V_{\text{max}}}{\text{flow rate}} \]](https://img.qammunity.org/2022/formulas/mathematics/college/gp6ry504drcglmfvwvsj5y0j83mzwj7zwq.png)
![\[ \text{Time (minutes)} = (523.8)/(2772) \]](https://img.qammunity.org/2022/formulas/mathematics/college/io0m1wb3lf3kzq1x2yqxf0rdewksdmomw4.png)
![\[ \text{Time (minutes)} \approx 0.1890 \, \text{minutes} \]](https://img.qammunity.org/2022/formulas/mathematics/college/bzx1ttih7oguy2nmxmlor3zwnt2a8qvvdv.png)
Convert the time to seconds:
![\[ \text{Time (seconds)} = \text{Time (minutes)} * 60 \]](https://img.qammunity.org/2022/formulas/mathematics/college/9xesmqfzvfp8luvbujyc68byr9f0b7zlf8.png)
![\[ \text{Time (seconds)} \approx 11.34 \, \text{seconds} \]](https://img.qammunity.org/2022/formulas/mathematics/college/l3f58nu8peb54vhn9rmunpr8wbpe553e36.png)
So, Ross can fill the water balloon for approximately 11.34 seconds before it pops, given the constraints.