The wavelength of light with an energy of
 is approximately
is approximately
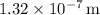 .
.
To find the wavelength
 of light given its energy
of light given its energy
 , you can use the following formula:
, you can use the following formula:
![\[ E = h \cdot \\u \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/uc05ymwnumftazyxmcjvcvi7dehgjzrjky.png)
Since
 can also be expressed as
can also be expressed as
 (where
(where
 is Planck's constant and
is Planck's constant and
 is the speed of light), we can set up the equation:
is the speed of light), we can set up the equation:
![\[ hc/\lambda = E \]](https://img.qammunity.org/2024/formulas/chemistry/college/bo4qg6xy3c8pof9krggvzpgt0ms46d4reo.png)
Solving for
 :
:
![\[ \lambda = (hc)/(E) \]](https://img.qammunity.org/2024/formulas/chemistry/college/6ogrh4la83c892ep3fejkeslvzx25aksqt.png)
Given
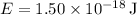 ,
,
 , and
, and
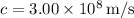 , you can substitute these values into the equation:
, you can substitute these values into the equation:
![\[ \lambda = \frac{(6.626 * 10^(-34) \, \text{J} \cdot \text{s}) \cdot (3.00 * 10^8 \, \text{m/s})}{1.50 * 10^(-18) \, \text{J}} \]](https://img.qammunity.org/2024/formulas/chemistry/college/7uv40714n8yp2bs0etw3atoazpglz8c89y.png)
Calculate this expression to find the wavelength
 . The unit of wavelength will be meters.
. The unit of wavelength will be meters.
![\[ \lambda \approx (1.987 * 10^(-25))/(1.50 * 10^(-18)) \, \text{m} \]](https://img.qammunity.org/2024/formulas/chemistry/college/w0d30x1hvtj6xkkfxwzgr87qwa3v8lcan5.png)
![\[ \lambda \approx 1.32 * 10^(-7) \, \text{m} \]](https://img.qammunity.org/2024/formulas/chemistry/college/ktq4vrgjclj5pej8mzpcnzcosb4mb0hfyn.png)
So, the wavelength of light with an energy of
 is approximately
is approximately
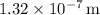 .
.
The probable question may be:
"What is the wavelength of light that has an energy of 1.50x
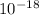 J "
J "