Question

Given: AD is an angle bisector of ∠BAC, AB ≅ AC

Prove: BD ≅ DC

a) ∠BDA ≅ ∠CDA; AB ≅ AC; ∠BAC is common ΔABD ≅ ΔACD by Angle-Angle-Side
b) ∠BDC ≅ ∠DBC; AB ≅ AC; ∠BAC is common ΔBDC ≅ ΔDBC by Angle-Angle-Side
c) ∠BAD ≅ ∠CAD; AB ≅ AC; ∠BAC is common ΔBAD ≅ ΔCAD by Angle-Angle-Side
d) ∠CDB ≅ ∠CBD; AB ≅ AC; ∠BAC is common ΔCDB ≅ ΔCBD by Angle-Angle-Side
e) ∠ABC ≅ ∠ACB; AB ≅ AC; ∠BAC is common ΔABC ≅ ΔACB by Angle-Angle-Side
f) ∠DAB ≅ ∠DAC; AB ≅ AC; ∠BAC is common ΔDAB ≅ ΔDAC by Angle-Angle-Side

Answer 1

Step-wise proof:

1.
`\( AD \) bisects \( \angle BAC \) (Given), so \( \angle BAD \cong \angle CAD \)`.

2.
`\( AB \cong AC \)` (Given).

3.
`\( AD \)` is common to both triangles
`\( ABD \)` and
`\( ACD \)` (Reflexive Property of Congruence).

4. Triangles
`\( ABD \)` and
`\( ACD \)` are congruent by ASA (Angle-Side-Angle).

5. By CPCTC (Corresponding Parts of Congruent Triangles are Congruent),
`\( BD \cong DC \)`.

Therefore, option f is correct

To prove that
`\( BD \cong DC \)`, we need to use the information given and find a congruence postulate or theorem that justifies the segments are congruent.

Given:

-
`\( AD \)` is an angle bisector of
`\( \angle BAC \)`, which means
`\( \angle BAD \cong \angle CAD \)`.

-
`\( AB \cong AC \)`.

To prove:

-
`\( BD \cong DC \)`.

Let's look at the potential congruences to see which one leads to the proof:

a)
`\( \angle BDA \cong \angle CDA \)`;
`\( AB \cong AC \)`;
`\( \angle BAC \)` is common
`\( \Delta ABD \cong \Delta ACD \)` by Angle-Angle-Side.

This option cannot be correct immediately because
`\( \angle BDA \)` and
`\( \angle CDA \)` are not necessarily congruent by the given information.

b)
`\( \angle BDC \cong \angle DBC \)`;
`\( AB \cong AC \)`;
`\( \angle BAC \)` is common
`\( \Delta BDC \cong \Delta DBC \)` by Angle-Angle-Side.

This option is not valid because it incorrectly identifies triangles and the angle relationships do not arise from the given information.

c)
`\( \angle BAD \cong \angle CAD \)`;
`\( AB \cong AC \)`;
`\( \angle BAC \)` is common
`\( \Delta BAD \cong \Delta CAD \)` by Angle-Angle-Side.

This option is incorrect because it talks about congruence between angles instead of segments.

d)
`\( \angle CDB \cong \angle CBD \)`;
`\( AB \cong AC \); \( \angle BAC \) is common \( \Delta CDB \cong \Delta CBD \)` by Angle-Angle-Side.

This option is not valid for the same reason as option b, it incorrectly identifies triangles and does not use the given information properly.

e)
`\( \angle ABC \cong \angle ACB \)`;
`\( AB \cong AC \)`;
`\( \angle BAC \)` is common
`\( \Delta ABC \cong \Delta ACB \)` by Angle-Angle-Side.

This option is true due to the Isosceles Triangle Theorem (since
`\( AB \cong AC \)`, the base angles
`\( \angle ABC \)` and are congruent), but it does not directly prove that
`\( BD \cong DC \)`.

f)
`\( \angle DAB \cong \angle DAC \)`;
`\( AB \cong AC \)`;
`\( \angle BAC \)` is common
`\( \Delta DAB \cong \Delta DAC \)` by Angle-Angle-Side.

This option is the correct reasoning. Since
`\( AD \)` bisects
`\( \angle BAC \)`, the angles
`\( \angle DAB \)` and
`\( \angle DAC \)` are congruent. We are also given that
`\( AB \cong AC \)`, and by the Reflexive Property,
`\( AD \cong AD \)`. Therefore, by Angle-Side-Angle (ASA) congruence postulate,
`\( \Delta ABD \cong \Delta ACD \).`

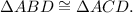
Step-wise proof:

1.
`\( AD \) bisects \( \angle BAC \) (Given), so \( \angle BAD \cong \angle CAD \)`.

2.
`\( AB \cong AC \)` (Given).

3.
`\( AD \)` is common to both triangles
`\( ABD \)` and
`\( ACD \)` (Reflexive Property of Congruence).

4. Triangles
`\( ABD \)` and
`\( ACD \)` are congruent by ASA (Angle-Side-Angle).

5. By CPCTC (Corresponding Parts of Congruent Triangles are Congruent),
`\( BD \cong DC \)`.

Therefore, the correct statement that describes the solution is:

f)
`\( \angle DAB \cong \angle DAC \)`;
`\( AB \cong AC \)`;
`\( \angle BAC \)` is common
`\( \Delta DAB \cong \Delta DAC \)` by Angle-Angle-Side.