Final Answer:
The range is (-∞, 0).
The correct option is c) (-∞, 0)
Step-by-step explanation:
The composition of functions
 is found by taking the function
is found by taking the function
 . Mathematically, this is expressed as
. Mathematically, this is expressed as
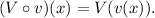
Given
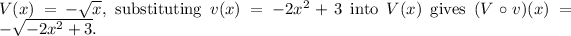
To determine the range of
 we need to analyze the behavior of the inner function
we need to analyze the behavior of the inner function
 under the square root. The expression
under the square root. The expression
 represents a downward-facing parabola, and the square root of this expression is defined for values where
represents a downward-facing parabola, and the square root of this expression is defined for values where

Solving

However, since we are looking for the range of
 the negative square root introduces an additional negation. Therefore, the range is
the negative square root introduces an additional negation. Therefore, the range is
 . This means that for any valid input
. This means that for any valid input
 will produce a value less than or equal to zero.
will produce a value less than or equal to zero.
The correct option is c) (-∞, 0)