Question

The derivative of the function \(f\) is given by \(f'(t) = 8e^{0.2\cos(t)}\) and \(f(2.2) = 4.5\). If the linear approximation:

A. Apply the linear approximation formula to estimate function values.
B. Discuss the role of the derivative in linear approximations.
C. Evaluate the accuracy of the linear approximation.
D. Analyze the implications of the given information on the function.

Answer 1

A. Applying the linear approximation formula using the given information, the estimated value of
`\(f(2.4)\) is \(4.5 + 2 * 8e^(0.2\cos(2.2))\)`(Option A).

Step-by-step explanation:

A. The linear approximation formula is given by
`\(L(t) = f(a) + f'(a) \cdot (t - a)\)`. Substituting
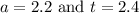`\(a = 2.2\) and \(t = 2.4\)` with the provided values, the estimated value of
`\(f(2.4)\) is \(4.5 + 8e^(0.2\cos(2.2)) * (2.4 - 2.2) = 4.5 + 2 * 8e^(0.2\cos(2.2))\).`

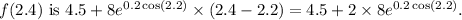
B. The derivative
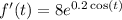`\(f'(t) = 8e^(0.2\cos(t))\)` represents the instantaneous rate of change of
`\(f(t)\)`. In linear approximations, the derivative is crucial as it provides the slope of the tangent line at a given point. This slope is then used to estimate the change in the function for small variations in
`\(t\).`

C. To evaluate the accuracy of the linear approximation, one can compare the estimated value obtained from the linear approximation formula with the actual function value at
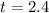`\(t = 2.4\)`. This comparison helps assess how well the linear approximation captures the local behavior of the function around
`\(t = 2.2\).`

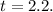
D. The given information about
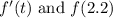`\(f'(t)\) and \(f(2.2)\)` offers insights into the behavior of the function near
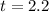`\(t = 2.2\)`. The linear approximation utilizes this information to estimate the function's values in the neighborhood of
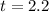`\(t = 2.2\)`, providing a linear model that aids in understanding the function's behavior in the vicinity of the given point.

So correct option is (Option A).