Expressing
 in terms of
in terms of
 yields
yields
 This simplification utilizes multiple angle formulas for cosine and double-angle identities.
This simplification utilizes multiple angle formulas for cosine and double-angle identities.
![\[ \cos(6x) = 4(2\cos^2(x) - 1)^3 - 3(2\cos^2(x) - 1) \]](https://img.qammunity.org/2024/formulas/mathematics/college/gsusmrxfevvj7a5456lwvypkjbi59ytjhh.png)
let's express
 using the double-angle formula:
using the double-angle formula:
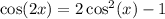
Substituting
 into the equation for
into the equation for
 :
:
![\[ \cos(6x) = 4(\cos(2x))^3 - 3\cos(2x) \]](https://img.qammunity.org/2024/formulas/mathematics/college/6kkq9bxibi8ef2ma4n73b2oxqoqu8xmjl0.png)
let's express
 again in terms of
again in terms of
 :
:
![\[ \cos(2x) = 2\cos^2(x) - 1 \]](https://img.qammunity.org/2024/formulas/mathematics/college/zne9htkhoqd1qbpbc9omclylgkfcm5ezzv.png)
Substitute this back into the equation for
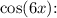
![\[ \cos(6x) = 4(2\cos^2(x) - 1)^3 - 3(2\cos^2(x) - 1) \]](https://img.qammunity.org/2024/formulas/mathematics/college/gsusmrxfevvj7a5456lwvypkjbi59ytjhh.png)
Expanding the cube term
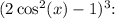
![\[ \cos(6x) = 4(8\cos^6(x) - 12\cos^4(x) + 6\cos^2(x) - 1) - 6\cos^2(x) + 3 \]](https://img.qammunity.org/2024/formulas/mathematics/college/k15yfpdvifx6ah1grigk2ku09zoh9rcg9s.png)
Simplifying further:
![\[ \cos(6x) = 32\cos^6(x) - 48\cos^4(x) + 24\cos^2(x) - 4 - 6\cos^2(x) + 3 \]](https://img.qammunity.org/2024/formulas/mathematics/college/q2blbb1f7hzive0x35eo1zsrnbq2pu8ia9.png)
Combine like terms:
![\[ \cos(6x) = 32\cos^6(x) - 48\cos^4(x) + 18\cos^2(x) - 1 \]](https://img.qammunity.org/2024/formulas/mathematics/college/gjigmec43vw8igeujezdjuyx1fwukj2kjs.png)
Hence,
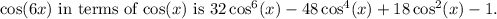
complete the question
Simplify the expression
 in terms of
in terms of
