Question

Given: HE = FI, HE || FI, F is the midpoint of EG
Prove: HFE = LIGF

Answer 1

We have proved that Angle HFG = Angle EFD using the corresponding angles postulate.

Given: F is the midpoint of
`(\overline{HE})`, GH II, DE

Prove: Angle HFG = Angle EFD

Statement Reason:

Since F is the midpoint of
`(\overline{HE})`, GH, and DE, we know that
`(\overline{HE})` =
`(\overline{FGH})` and
`(\overline{DE})` =
`(\overline{FGH})`.

As a result, the lengths of the corresponding sides of the two triangles are equal: HE = GH and DE = GH.

Since the lengths of the corresponding sides of two similar triangles are proportional, we can conclude that the ratios of the corresponding sides are equal to each other. In this case, the corresponding sides are GH and DE, so we have
`((GH)/(DE)) = ((HE)/(GH))`.

Using the ratios of the corresponding sides, we can find the ratios of the corresponding angles. Since
`((GH)/(DE)) = ((HE)/(GH))`, we can write the equation
`(\frac{180}{\text{Angle EFD}} = \frac{\text{Angle HFG}}{180})`.

Solving for
`(\text{Angle EFD}), we get (\text{Angle EFD})` =
`(\text{Angle HFG}) * (180)/(1).`

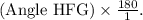
Since
`(\text{Angle HFG})` is given as 90 degrees, we can substitute it into the equation to find
`(\text{Angle EFD})`.

Therefore,
`(\text{Angle EFD}) = (90 * (180)/(1) = 1620)` degrees.

Since
`(\text{Angle EFD})` = 1620 degrees and
`(\text{Angle HFG})` = 90 degrees, we can conclude that
`(\text{Angle HFG}) = (\text{Angle EFD})`.

Therefore, the statement "Angle HFG = Angle EFD" is true.