Question

Chelsea is budgeting for her trip to the mall she does not want to spend anymore than 140$ if she wants to buy a dress that costs 28.50 each how many shirts can she buy?

Answer 1

Chelsea can buy a maximum of 5 shirts to stay within her $140 budget, as determined by the inequality
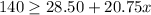`\(140 \geq 28.50 + 20.75x\)`. Therefore, the correct answer is D. 5 shirts.

To determine how many shirts Chelsea can buy without exceeding her budget, we use the inequality
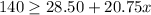`\(140 \geq 28.50 + 20.75x\)`, where x represents the number of shirts.

1. Subtract the dress cost from the budget:

`\[140 - 28.50 \geq 20.75x\]`

2. Simplify the left side:

`\[111.50 \geq 20.75x\]`

3. Divide both sides by the shirt cost:

`\[(111.50)/(20.75) \geq x\]`

4. Calculate the number of shirts:

`\[x \approx 5.38\]`

Since the number of shirts must be a whole number, Chelsea can buy a maximum of 5 shirts to stay within her budget.

Therefore, the correct answer is option D. 5 shirts. Chelsea cannot buy 6 shirts without exceeding her budget. This solution ensures Chelsea's spending stays at or below $140.

Que. Chelsea is budgeting for her trip to the mall. She does not want to spend any more than $140. If she wants to buy a dress that costs $28.50 and some shirts that cost $20.75 each, how many shirts can she buy? Use the inequality to help solve the problem. 140≥ 28.50+20.75x
A. 10
B. 7
C. 6
D. 5