Question

Find the absolute maximum and minimum values of f(x) = 2x³ - 9x² - 60x + 4 on the interval [-3, 1].

Answer 1

• The absolute maximum value of
  `f(x)` on interval
  `[-3,1]` is
  `72` at
  `x=-2`.
• The absolute minimum value of
  `f(x)` on interval
  `[-3,1]` is
  `-63` at
  `x=1`.

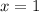Step-by-step explanation:

To find the absolute maximum and minimum values of the function
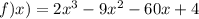`f)x)=2x^(3)-9x^2-60x+4` on the interval
`[-3,1]`, we'll follow these steps:

1. Find the Derivative: This will help us locate the critical points, where the slope of the function is zero or undefined.
2. Identify Critical Points: Solve
   `f'(x)=0` and check for any points where
   `f'(x)` is undefined.
3. Evaluate the Function at Critical Points and Endpoints: We'll plug these points into
   `f(x)` to find the corresponding y-values.
4. Determine the Absolute Maximum and Minimum: The highest and lowest y-values from step 3 are the absolute maximum and minimum, respectively.

Let's start by finding the derivative of
`f(x)`.

Step 1: Find the Derivative

`f(x)=2x^3-9x^2-60x+4`

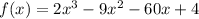
The derivative,
`f'(x)`, is:

`f'(x)=(d)/(dx)(2x^3)- (d)/(dx)(9x^2)-(d)/(dx)(60x)+(d)/(dx)(4)`

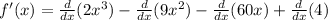
Now, let's calculate this derivative.

The derivative
`f'(x)` is:

`f'(x)=6x^2-18x-60`

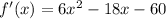
Step 2: Identify Critical Points

To find the critical points, we solve
`f'(x)=0`. This means we need to solve the equation:

`6x^2-18x-60=0`

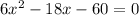
Let's solve this quadratic equation for
`x`.

The critical points are
`x=-2` and
`x=5`. However, since we are only interested in the interval
`[-3,1]`, we can ignore
`x=5` as it is outside this range.

Step 3: Evaluate the Function at Critical Points and Endpoints

We need to evaluate
`f(x)` at the critical point
`x=-2` and the endpoints of the interval,
`x=-3` and
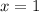`x=1`. This will give us the function values at these points.

Let's calculate
`f(-2)`,
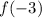`f(-3)`, and
`f(1)`.

The function values at the critical point and endpoints are:

• 
  `f(-2)=72`
• 
  `f(-3)=49`
• 
  `f(1)=-63`

Step 4: Determine the Absolute Maximum and Minimum

• The absolute maximum value of
  `f(x)` on interval
  `[-3,1]` is
  `72` at
  `x=-2`.
• The absolute minimum value of
  `f(x)` on interval
  `[-3,1]` is
  `-63` at
  `x=1`.

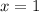These are the highest and lowest values the function attains in the given interval.