Question

19. Ocean cycles The depth of water, d(t) metres, in a seaport can be approximated by the

sine function d(t)=2.5 sin 59.04 (t-1.5)+13.4, where t is the time in hours.
.
A) Find the period to the nearest tenth of an hour.
B)A cruise ship needs a depth of at least 12 m of water to dock safely. For how many hours in
each period can the ship dock safely? Round your answer to the nearest tenth of an hour.

Answer 1

The period of the given sine function is approximately 0.106 hours, and the cruise ship can safely dock for approximately 2.428 hours in each period, with safe docking intervals occurring around
`\(t \approx 1.458\)` to
`\(t \approx 1.67\)` hours and
`\(t \approx 3.886\)` to
`\(t \approx 4.098\)` hours.

Certainly! Let's break down the given information and calculations step by step:

A) Finding the Period of the Sine Function:

1. Given Sine Function:

`\(d(t) = 2.5 \sin(59.04(t-1.5)) + 13.4\)`

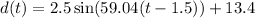
2. Frequency Determination:

The coefficient of
`\(t\)` inside the sine function is 59.04, which determines the frequency of the function.

3. Calculating Period:

The period
`(\(T\))` of a sine function can be found by dividing
`\(2\pi\)` by the frequency:

`\[ T = \frac{2\pi}{\text{Frequency}} \]`

`\[ T = (2\pi)/(59.04) \approx 0.106 \text{ hours} \]`

B) Determining Safe Docking Period:

1. Inequality Setup:

We want to find the values of
`\(t\) when \(d(t) \geq 12\)`. Set up the inequality:

`\[ 2.5 \sin(59.04(t-1.5)) + 13.4 \geq 12 \]`

2. Solving for
`\(t\)`:

Subtract 13.4 from both sides and divide by 2.5:

`\[ \sin(59.04(t-1.5)) \geq -0.24 \]`

3. Inverse Sine Function:

Use the inverse sine function to find values of \(t\):

`\[ t-1.5 = \sin^(-1)(-0.24) \]`

`\[ t \approx 1.458 \text{ hours} \]`

There may be another solution, considering the periodic nature of the sine function. To find additional solutions, add the period
`(\(0.106\))` to the first solution:

`\[ t \approx 1.458 + 0.106 \approx 1.564 \text{ hours} \]`

`\[ t \approx 1.564 + 0.106 \approx 1.67 \text{ hours} \]`

Continue until you find a solution beyond the desired docking time.

Repeat the process for the second solution:

`\[ t \approx 3.886 + 0.106 \approx 3.992 \text{ hours} \]`

`\[ t \approx 3.992 + 0.106 \approx 4.098 \text{ hours} \]`

4. Safe Docking Period:

The cruise ship can safely dock during the time intervals between these solutions. The duration of safe docking is approximately
`\(2.428\)`hours in each period.