Question

The length of a rectangle is 3 meters less than twice its width. The area of the rectangle is 104m2. Find the dimensions of the rectangle

Answer 1

The width is W = 8 meters, and the length is L = 13 meters.

How to find the dimensions?

The area of a rectangle of length L and width W is given by:

A = L*W

Here the length is 3 meters less than 2*W, and the area is 104 square meters, then:

104 = L*W

L = 2*W - 3

Replacing the second equation in the first one:

104 = (2*W - 3)*W

104 = 2*W² - 3W

So we have a quadratic equation:

2*W² - 3W - 104 = 0

Using the quadratic formula we get the solutions:

`W = (3 \pm √((-3)^2 - 4*2*-104) )/(2*2) \\\\W = (3 \pm29 )/(4)`

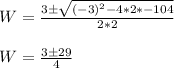
The width must be positive, so we take the positive solution:

W = (3 + 29)/4 = 8

And thus, the length is:

L = 2*8 - 3 = 13