Question

Given Оо x³-1 x²-1 -/32/3 m/N 3 X-1 O DNE for x < 1 [, for x ≥ 1 . What is lim f(x)? x-1-​

Answer 1

The limit of the given piecewise function f(x) as x approaches 1 does not exist (DNE) because the left-hand limit is
`\((3)/(2)\)`, and the right-hand limit is infinity, indicating a discontinuity at x = 1. The correct answer is (d) DNE.

To find
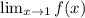`\(\lim_{{x \to 1}} f(x)\)` for the piecewise function f(x), we need to evaluate the left-hand limit (
`\(\lim_{{x \to 1^-}} f(x)\)`) and the right-hand limit (
`\(\lim_{{x \to 1^+}} f(x)\)`).

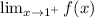For x < 1, the expression is
`\(\frac{{x^3 - 1}}{{x^2 - 1}}\).`

For
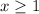`\(x \geq 1\)`, the expression is
`\(\frac{3}{{x - 1}}\).`

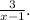
Let's calculate the left-hand limit:

`\[\lim_{{x \to 1^-}} f(x) = \lim_{{x \to 1^-}} \frac{{x^3 - 1}}{{x^2 - 1}}\]`

To evaluate this limit, we can factor the numerator and denominator:

`\[= \lim_{{x \to 1^-}} \frac{{(x - 1)(x^2 + x + 1)}}{{(x - 1)(x + 1)}}\]`

Now, cancel out the common factor (x - 1):

`\[= \lim_{{x \to 1^-}} \frac{{x^2 + x + 1}}{{x + 1}}\]`

Plugging in x = 1, we get
`\((3)/(2)\).`

Now, let's calculate the right-hand limit:

`\[\lim_{{x \to 1^+}} f(x) = \lim_{{x \to 1^+}} \frac{3}{{x - 1}}\]`

Plugging in x = 1, we get
`\(\infty\)` (because the denominator approaches zero from the positive side).

Since the left-hand limit and right-hand limit do not match,
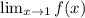`\(\lim_{{x \to 1}} f(x)\)` does not exist (DNE). Therefore, the correct answer is (d) DNE.