Final answer:
To solve the equation 5e^(4a+2)=40 for a, divide both sides by 5, take the natural logarithm of both sides, solve for a, and round a to four decimal places. The approximate value of a is 0.0198.
Step-by-step explanation:
To solve for a in the equation
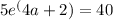
, we first isolate the exponential term by dividing both sides of the equation by 5:
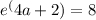
Next, we take the natural logarithm of both sides to eliminate the exponent, which gives us:
4a+2 = ln(8)
Then we solve for a by subtracting 2 from both sides and dividing the result by 4:
a = (ln(8) - 2) / 4
Now we can enter the data into a calculator to find the value of a, rounded to four decimal places:
a ≈ (2.0794 - 2) / 4 ≈ 0.0794 / 4 ≈ 0.0198
So, the approximate value for a, rounding to four decimal places, is 0.0198.
It's important to express the final answer to the proper number of significant figures. To understand significant figures, here are some examples using the given SEO keywords:
- For the calculation of 22.4 × 8.314, the answer should be rounded to the least number of significant figures in the given values, which is three significant figures, yielding approximately 186.
- For 0.424 rounded to two significant figures, the result is 0.42.
- For 0.0038661 rounded to three significant figures, the result is 0.00387.