Question

1. Hydrogen: For an electron in the lowest energy it can orbit around proton, they have a separation of 5.3 *10-11 m. If you have a 4.5*10-19J photon (bit of light) hit the electron, it will transfer all of its energy to the proton electron interaction and the electron will start orbiting at a larger radius. Assuming all the energy went into the potential energy, what is the new distance between the electron and proton.

Answer 1

rₙ = 1,325 10⁻⁹ m

Step-by-step explanation:

To solve this problem we use the bohr atomic model

Eₙ = -13.606 /n² [eV]

the brackets indicate that the units are in electron volts.

let's reduce the photon energy to eV

E = 4.5 10-19J (1 eV / 1.6 10⁻¹⁹ eV) = 2.8125 eV

This energy is in the visible range, so the transition must occur in this range, this is for the Balmer series whose initial number is n₀ = 2

for an atomic transition on two levels

ΔE = Eₙ - E₀ =
`(-13.606)/(n^2) + (13.606)/(2^2)`

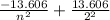
2.8125 =
`(-13.606)/(n^2) + 3.4015`

`(13.606)/(n^2)` = 3.4015 - 2.8125 = 0.589

n² = 13.606 / 0.589

n² = 23.1

n = 4.8

as n must be an integer

n = 5

taking the quantum number as far as the electron goes, we substitute in the equation for the radius

rn = n² a₀

where ao is the radius of the lowest level a₀ = 5.3 10⁻¹¹ m

rₙ = 5 2 5.3 10⁻¹¹

rₙ = 132.5 10⁻¹¹ m

rₙ = 1,325 10⁻⁹ m