Question

The motion of a particle is given by î„î…î‡î„î…cosî„î€´î€½îƒ¸î… where  is in s. What is the first time at which the kinetic energy is twice the potential energy?

Answer 1

The first time at which the kinetic energy is twice the potential energy is when time (t) is given by
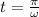`\( t = (\pi)/(\omega) \)\\`, where
`\( \omega \)` is the angular frequency of the motion.

Step-by-step explanation:

The motion of the particle is described by the equation
`\( x(t) = A \cos(\omega t) \)`, where x is the displacement, A is the amplitude, and
`\( \omega \)` is the angular frequency. The kinetic energy (KE) and potential energy (PE) for simple harmonic motion are given by the expressions:

`\[ KE = (1)/(2) m \omega^2 A^2 \sin^2(\omega t) \]`

`\[ PE = (1)/(2) m \omega^2 A^2 \cos^2(\omega t) \]`

To find when the kinetic energy is twice the potential energy, we set
`\( KE = 2 \cdot PE \)`:

`\[ (1)/(2) m \omega^2 A^2 \sin^2(\omega t) = 2 \cdot (1)/(2) m \omega^2 A^2 \cos^2(\omega t) \]`

Simplifying, we get
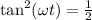`\( \tan^2(\omega t) = (1)/(2) \)`. Taking the arctangent of both sides, we find
`\( \omega t = (\pi)/(4) \).` Therefore,
`\( t = (\pi)/(4\omega) \).`

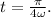
This result indicates that the first time at which the kinetic energy is twice the potential energy is
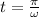`\( t = (\pi)/(\omega) \)`.