Question

The total cost of 3kg apples and 5 kg. oranges is Rs. 1080. If the cost of 3 kg. apples is the same as the cost of 7kg. oranges, find the cost of each kg. of both fruits.​

Answer 1

cost of apples = 210Rs cost of oranges = 90Rs

Explanation:

with the given we have we can write 2 equations

let a be the cost of apples and b the cost of oranges

3a + 5b = 1080 (The total cost of 3kg apples and 5 kg. oranges is Rs. 1080)

3a = 7b (the cost of 3 kg. apples is the same as the cost of 7kg. oranges)

substitute 3a with 7b in the first equation

7b + 5b = 1080

12b = 1080

b= 90

now find a

3a = 7b

3a = 90*7 = 630

a=630/3=210

Answer 2

⭐ Let "a" be the cost of each kg of apples and "o" be the cost of each kg of oranges.

⭐ First of all understanding all the question carefully, we can form two equation which can be given by,

• 3a + 5o = 1080 - - - (1)

(Total cost of 3kg apple and 5kg oranges is total about 1080Rs.)

• 3a = 7o - - - (2)

(Cost of 3kg of apples is equal as the same cost of 7kg of oranges)

Now we can substitute the value of (7o) instead of (3a) so as to collect the same variables. Substituting values,

`\Rrightarrow\bf{3a + 5o = 1080}`

`\Rrightarrow\bf{7o + 5o = 1080}`

`\Rrightarrow\bf{12o = 1080}`

`\Rrightarrow\bf{o = (1080)/(12) }`

`\Rrightarrow\bf{0 = 90}`

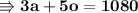
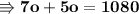
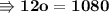
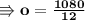
Now replacing value of (o = 90) in equation (2),

`\Rrightarrow\bf{3a = 7o}`

`\Rrightarrow\bf{3a = 7 * 90}`

`\Rrightarrow\bf{3a = 630}`

`\Rrightarrow\bf{a = (630)/(3) }`

`\Rrightarrow\bf{a = 210}`

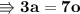
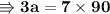
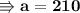
• Thus the values of each kg of apples are 210Kg and of oranges are 90Kg