Question

The mean number of hours of study time per week for a sample of 544 students is 21 . If the margin of error for the population mean with a 98% 98% confidence interval is 1.5 , construct a 98% confidence interval for the mean number of hours of study time per week for all students.

Answer 1

The 98% confidence interval for the mean number of study hours per week for all students is 19.5 to 22.5 hours, calculated by adding and subtracting the margin of error (1.5 hours) from the sample mean (21 hours).

Step-by-step explanation:

To construct a 98% confidence interval for the mean number of hours of study time per week for all students, we can use the mean and the margin of error provided.

The sample mean is 21 hours per week and the margin of error is 1.5 hours.

The confidence interval is found by subtracting the margin of error from the sample mean to find the lower bound and adding the margin of error to the sample mean to find the upper bound.

The confidence interval is therefore:

Lower Bound: 21 - 1.5 = 19.5 hours

Upper Bound: 21 + 1.5 = 22.5 hours

Thus, the 98% confidence interval for the mean number of study hours per week is 19.5 to 22.5 hours.

Answer 2

The 98% confidence interval for the mean number of hours of study time per week for all students is
`\(_(20.25)\)^(22.75) (20.25 to 22.75) hours.`

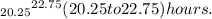
Step-by-step explanation:

To construct the 98% confidence interval, we use the formula:

`\[ \text{Confidence Interval} = \text{Sample Mean} \pm \left( \text{Margin of Error} * \text{Critical Value} \right) \]`

Given that the sample mean is
`\( \bar{x} = 21 \)` hours, and the margin of error is
`\( ME = 1.5 \)` hours, the critical value for a 98% confidence interval is found using statistical tables, and for a normal distribution, it is approximately 2.33.

Now, substitute these values into the formula:

`\[ \text{Confidence Interval} = 21 \pm \left( 1.5 * 2.33 \right) \]`

`\[ \text{Confidence Interval} = 21 \pm 3.495 \]`

Thus, the margin of error gives us the range within which we are confident the true population mean lies. So, the confidence interval is
`\(_(20.505)\)^(21.495).`

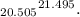
In conclusion, we are 98% confident that the true mean number of hours of study time per week for all students is between 20.505 and 21.495 hours. This means that if we were to take many samples and compute the 98% confidence interval for each, we would expect the true population mean to fall within these bounds for 98% of the intervals.