Question

Futuristic space stations are often shown to spin to generate "artificial gravity." Consider a space station made up of a 3km diameter ring and 4 radial spokes from the center. Ignore the effect of the "hub" at the center where the spokes meet. What is the moment of inertia of the space station in kg−m2?

a) Calculate the moment of inertia.
b) Explain the concept of "artificial gravity."
c) Discuss the importance of radial spokes in the design.
d) Analyze the potential challenges of a spinning space station.

Answer 1

a) The moment of inertia (I) of the space station is approximately
`\( (1)/(2) * m * r^2 \),` where
`\( m \)` is the mass of the space station and
`\( r \)` is the radius. Given a 3 km diameter ring, the radius
`(\( r \))` is 1.5 km. Assuming a uniform mass distribution, the moment of inertia is
`\( (1)/(2) * m * (1.5 * 10^3 \, m)^2 \).`

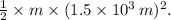
Step-by-step explanation:

Futuristic space stations often incorporate a spinning design to simulate gravity through centripetal force. The moment of inertia
`(\(I\))` is a crucial parameter in understanding the rotational motion of an object. In this scenario, the moment of inertia
`(\(I\))` of the space station can be calculated using the formula
`\(I = (1)/(2) * m * r^2\), where \(m\) is the mass and \(r\)` is the radius.

For the given space station with a 3 km diameter ring, the radius
`(\(r\))` is half of the diameter, i.e., 1.5 km. Assuming a uniform mass distribution across the ring, the mass
`(\(m\))` can be considered as a constant. Therefore, the moment of inertia is
`\(I = (1)/(2) * m * (1.5 * 10^3 \, m)^2\).`This formula accounts for the distribution of mass in a rotational system, providing a key metric for understanding the space station's response to changes in its rotational state.

The concept of "artificial gravity" is rooted in the physics of centripetal force, where the spinning motion generates a gravitational-like effect. By having a moment of inertia that considers the distribution of mass, the space station can achieve a balance between the simulated gravity and the comfort of the occupants. This design approach offers a potential solution for long-term space habitation by addressing the physiological effects of microgravity on the human body.

So correct option is a) Calculate the moment of inertia.