Final Answer:
The answer of the given equation is "the degree and zeros of the polynomial f(x) = (x - 1)(x + 1)" is a. Degree 2; zeros 1, -1
Step-by-step explanation:
The polynomial
 can be expanded to
can be expanded to
 The degree of a polynomial is the highest power of the variable present. In this case, the highest power of
The degree of a polynomial is the highest power of the variable present. In this case, the highest power of
 is 2, so the degree is 2.
is 2, so the degree is 2.
To find the zeros, set
 equal to zero and solve for
equal to zero and solve for
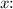
![\[x^2 - 1 = 0\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8jcz0afjwewmo0yrsdd76e0lb802xcczn7.png)
This equation has solutions when
 and
and
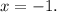 Therefore, the zeros of the polynomial are 1 and -1.
Therefore, the zeros of the polynomial are 1 and -1.
In summary, the correct answer is a. Degree 2; zeros 1, -1.