Question

A line makes a 74.78 degree angle with the x-axis and goes through the point (0,7). What is the function of the line? (Round your slope ratio to the nearest tenth.)

Answer 1

Check the picture below.

so we can pretty much see that the rise = 7, let's find the run "z" to get its slope.

`\tan(74.78^o )=\cfrac{\stackrel{opposite}{7}}{\underset{adjacent}{z}} \implies z\tan(74.78^o)=7 \\\\\\ z=\cfrac{7}{\tan(74.78^o)}\implies z\approx 1.9`

so z = 1.9, and since "z" is in the II Quadrant that makes it -1.9, so now, we can say, what's the equation of a line that passes through (0 , 7) and (-1.9 , 0)

`(\stackrel{x_1}{0}~,~\stackrel{y_1}{7})\qquad (\stackrel{x_2}{-1.9}~,~\stackrel{y_2}{0}) ~\hfill~ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{0}-\stackrel{y1}{7}}}{\underset{\textit{\large run}} {\underset{x_2}{-1.9}-\underset{x_1}{0}}} \implies \cfrac{ -7 }{ -1.9 } \approx 3.7`

`\begin{array} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{7}\approx\stackrel{m}{3.7}(x-\stackrel{x_1}{0}) \\\\\\ y-7\approx 5x\implies {\Large \begin{array}{llll} y \approx 3.7x+7 \end{array}}`

Answer 2

The equation of the line is y≈3.3x+7.

The slope of the line is equal to the tangent of the angle it makes with the positive x-axis.

Therefore, the slope of the line is equal to tan(74.78 ∘ )≈3.3.

The y-intercept of the line is 7, since the line passes through the point (0,7).

Therefore, the equation of the line is y≈3.3x+7.

Here are the steps to solve for the equation of the line:

Recall the formula for the slope of a line: m=
`(y_(2)- y_(1) )/(x_(2) -x_(1))`

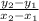
, where (
`x_(1)`,
`y_(1)` ) and (​
`x_(2)` ,
`y_(2)` ) are two points on the line.

Use the given angle to find the slope: Since the line makes a 74.78-degree angle with the positive x-axis, the slope is equal to

tan(74.78∘ )≈3.3.

Use the given point to find the y-intercept: Since the line passes through the point (0,7), the y-intercept is 7.

Substitute the slope and y-intercept into the equation of the line: y=mx+b, where m is the slope and b is the y-intercept. In this case, the equation is y≈3.3x+7.

Therefore, the equation of the line is y≈3.3x+7.