Question

Tor out the greatest com 7x^(4)+21x^(3)

Answer 1

The greatest common factor of the expression
`\(7x^4 + 21x^3\) is \(7x^3\).`

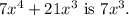
Step-by-step explanation:

To find the greatest common factor (GCF) of
`\(7x^4 + 21x^3\),` we look for the highest power of \(x\) that divides both terms. In this case,
`\(7x^3\)` is the greatest common factor. By factoring out
`\(7x^3\)`, we get
`\(7x^3(x + 3)\)`. The process involves dividing each term by
`\(7x^3\),` resulting in the factored form.

The GCF is found by identifying the largest power of the common factor present in both terms. In
`\(7x^4 + 21x^3\), \(x^3\)` is the highest power that divides both terms evenly. Factoring out
`\(7x^3\)` leaves us with the simplified expression
`\(7x^3(x + 3)\)`, where
`\(x + 3\)` represents the remaining factor after factoring out the GCF.

This method is essential for simplifying algebraic expressions and equations by factoring out common factors. It allows us to rewrite complex expressions in a more concise form, making it easier to analyze and work with. In this case, factoring out the GCF helps reveal the underlying structure of the expression, making it more manageable for further mathematical operations or analysis.