Answer:
D
Explanation:
The income is given by:
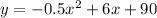
And the costs are given by:

Where x is the number of units sold, in hundreds, and y is the total dollar amount, in thousands.
We want to find a viable solution for the number of units sold that would cause the income and cost to be the same.
So, we can set the two equations equal to each other and solve for x. Therefore:
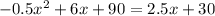
Subtract 2.5x and 30 from both sides:
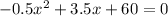
Remove the decimals and the negative of the leading coefficient by multiply both sides by -2:
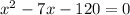
Factor. We can use -15 and 8. So:
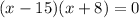
Zero Product Property:
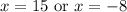
The answer must be positive since we cannot sell negative units.
So, the value of x is:
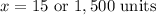
Then using either equation, the value will be:
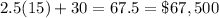
Our answer is D.