Answer:
A zero of a function is a number, when plugged in for the variable, makes the function equal to zero.
Then, the roots of a polynomial P(x) are values of x such that P(x) = 0.
Given the polynomial function:
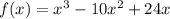
By the rational theorem process, gives us the following possible roots: 0,
 ,
,
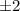 ,
,
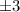 ,
,
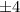 ,
,
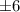 ,
,
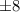 ,
,
 and
and
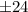
for x =0
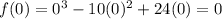
Now, our polynomial become:
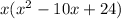 = 0
= 0
Then, we factors the remaining quadratic equation, factoring by grouping , using the facts 4+6 = 10 and
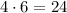
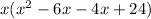 = 0
= 0
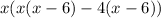 =0
=0
 =0
=0
Zero product property states that if xy = 0 then either a =0 or b =0.
by zero product property;
⇒ x = 0, x-6=0 and x-4 = 0
Hence, x = 0 , x = 4 and x =6 are the zeros of the given polynomial function.