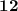If the quadratic is a perfect square, then there has to be a way to write the quadratic as
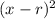
, where

is a root of the equation. Expanding it out, we see that

Now let's compare this form to the one that we were given. Since

matches up with

,

has to equal either

or

. So, since
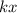
in the original equation matches up with
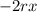
in the equation we found,

and
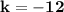
or