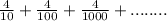Question

Which geometric series represents 0.4444... as a fraction?

Answer 1

The geometric series that represents 0.4444... as a fraction is: 4/6 * [k=0, ∞]∑1/6^k

Answer 2

Answer: It can be expressed as

`(4)/(10)+(4)/(100)+(4)/(1000)+........`

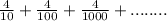
Explanation:

Since we have given that 0.44444.......

We need geometric series that represents as a fraction.

so, it can be written as

0.4+0.04+0.004+0.0004...............

But as we are required to write it as a fraction , So, it becomes,

`(4)/(10)+(4)/(100)+(4)/(1000)+(4)/(10000)............`

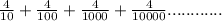
and it is a geometric series.

Because it has first term = a =
`(4)/(10)`

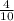
and common ratio = r =
`(a_2)/(a_1)=((4)/(100))/((4)/(10))=(1)/(10)`

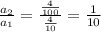
Hence, it can be expressed as

`(4)/(10)+(4)/(100)+(4)/(1000)+........`